Resonant Neuron Synthesis
The attempt for a new sound generation
introduced by Jürgen Michaelis
INDEX
Introduction
Step 1.The neural net
Step 2. The resonant filter
Step 3. The resonant neuron - Synthesis of step 1 and 2
Step 4. Complexity of system dynamics
Step 5. the multiplicative network by FM
Summary of the analog neuron level
Step 6. The digital sound code network
Final Summary of Resonant Neurons
Final statement
Introduction
At the beginning of the 21. century there is a clear trend in all areas of science and technology: a departure from the old cartesianic, linear and determinable world view. The new paradigmas are named complexity, order from chaos, self organisation of complex systems, networking and cooperation. A new math of complexity is under way to evolve, powered by new knowledge in biology, information technology and quantum physics.
It shows up that to capture nature by numerical mathematics is not that easy as it was thought of by the classical advocates of the mechanistic and reductionistic view. From a certain complexity onwards a system is not even the sum total of its parts but a greater whole which gains totally new attributes than its sub structures.
Also in cultural spheres of society those new thoughts push forward. Who hasn't heard about neural nets yet, which as technical pendants to the biological predecessor should teach the actually stupid, static and serial working computers the creative "thinking". Currently quite simple models are used to simulate the biological processes in neurons, axons and synapses.
Why not use these thoughts for the development of a new sound generation? A modulation path can be seen e.g. as a branch of a neural net, too. A signal can be a discrete voltage or a frequency or a sound or an oscillator. At last, the only question is in which context of time you see (and hear) those things.
.
A classical important part of acoustic, electronic and musical sounds in general is the sound filter which can filter parts of the signal as gain certain frequency areas by resonance. Thus the filter can be used for sound influence likewise as a sound source by self resonance. Just in modern music the filter has gained an extraordinary state of importance.
Yet it seems that in contemporary electronic music, the filter sound seems to influence the music more than the harmonic-compositionary component. Sound is complexity, and static beings like sine waves or stiff sound samples do not sound. Right through the modulation and the interdependent interaction the organic hearable sound arises.
The physicist and natural philosopher Friedrich Cramer has claimed the so-called resonance hypothesis, after which matter and the cosmic principle itself is an ever going (ongoing)(durating) form of this resonance thinking. Everything comes from resonances - lately the swing modes (spins) of elemetary particles and wave likelihoods of electron traces are resonances of certain energy spectrums. It is not strange, since resonance is physically a state of least energy and maximum gain (like resonant catastrophy), and everything in nature follows the strategy of least energy (or effect).
Even the hot discussed string theory which tries to explain the lowest levels of matter, claims there are "strings" (or newest M-branes) oscillating in a multi-dimensional tiny bended space rather than particles like points. First by the manifestation of a swinging, resonant "something", theoreticians could get rid of the many contradictions between quantum physics (micro cosmos) and relativity theory (macro cosmos). Because this theory is still under highest development, we can be curious what future results of this research will bring up to daylight.
Though it seems to be like Joachim Ernst Behrend postulated in his work:
Nada Brahma - the world is sound.
Seen in informational context, two systems in resonance represent the most simple way to transfer information from one system to the other - they do this in real time and with least possible energy consumption.
You can develop this principle of resonance in any level of our beings - also biological evolution is seen today more as a co-evolution rather than just the darwinistic fight of the stronger to the weaker (or the better adapted to the less adapted). The development of higher organized and specialized species is not only done by mutation and selection, but more driven by cooperation - you could name this also as "social resonance" -, symbiosis and self-organizing and cognitive processes of the whole system "Live".
All natural mutations alone would not have led to the extraordinary diversity and the extremly networked system Live on earth. There seems to be a "force" to drive the universe to higher levels of complexity, that cannot be explained only by mutation and selection like hardliner-darwinists propagate. Such systems however, tend to act in way that an evolution nische brakes the diversification and makes it very hard to step out of that niche.
That is happens though, our presence on this planet is the best prove for. By our ability to communicate we thrusted open a gate to our mental-social evolution and provided a strong power in development, maybe the strongest ever. Imagine the mental evolution would only be the game of mutation (trial) and selection (error) - we would certainly not be as far as we are. We are indeed learning from each other and together. I don't claim that the darwinistic theory is wrong - but it is not the only and the whole truth.
In my opinion communication is a part of the holistic system live and cosmos in whole, and lately we all gained from a single swinging being - the cosmos is alive!
My thought was to transfer the scientific and mental-philosophical aspects into a musical sound production and to integrate the both most important points - namely networking and resonance, which are in social dimensions similar terms like communication and harmony. As a third big column in the resonant neuron synthesis I have integrated the ability for a sound code exchange between the "sonic cells", in which processing orders for certain sonic commands can evolve in the net like a genetic code.
I will introduce in this article the 3 main elements - neural net, resonant neuron (filter) and genetic sound code exchange within several sections and show the first technical realiziation, namely the "Resonator Neuronium".
Because I was always working close to the "natural" sound production, say analog versus digital/DSP based sound production, the realization of the Resonator Neuronium is also analog or better hybrid analog/digital (digital is the sound code exchange). The neurons are fully analog build and offer therefore the sonical attributes that are always so direct and powerful like it is needed for a musical or sonic instrument.
Step 1.The neural net
I assume that you have certain basic knowledge with technical neural nets because it would be way too much to explain all attributes of neural nets within this article.
A technical neural net has an output and any number of inputs, which input signals pi are weighted with multiplicands (intensitys) wi and being added together.
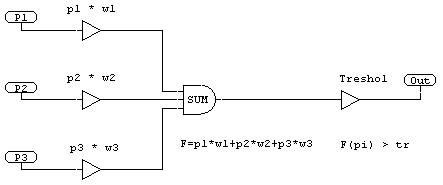
Pic. 1
The sum of all pi*wi is activated by a so-called threshold function and is then transferred to the output..
F = S(p0 pn) pi*wi |F>tr .
"tr" means threshold and defines the trigger level from which the function performes the wanted S-function. The threshold function can easiest act like a switch which transfers the sum onto the output (the neuron "fires") from a certain level onwards and below that level does nothing.
However, in praxis this unsteady function is problematic and is often replaced by a tangens hyperbolicus function which delivers a more continuous "flow of information" also at low levels because this function has no unsteadiness in the relevant area. So the main transfer function is superposed by a tangens hyperbolicus like a "windowing function":
Pic.2
The degree of networking is found by the connections of the outputs to the inputs of neighboured neurons to form so-called neuron layers. If you look at picture 3, you will find the maximum networking of n inputs = N number of neurons . A not used or wanted branch can be simply switched off by wi=0.
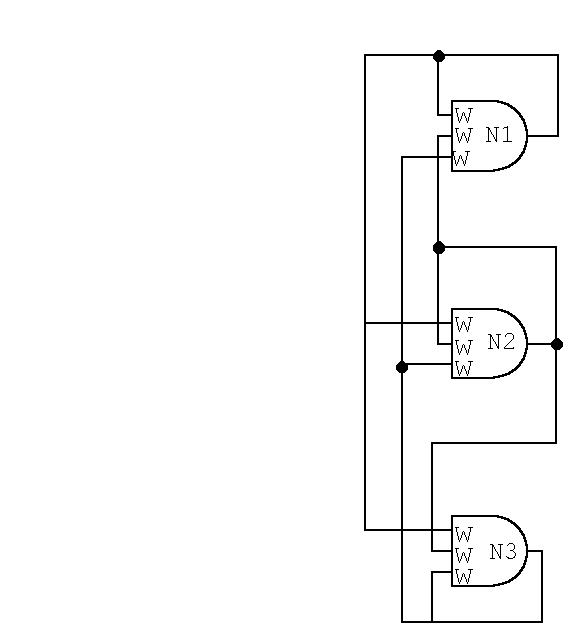
Pic. 3
Please note that the maximum topology of pic 3 includes self-connections for the neurons. This will be of greater importance in the later discussed resonant neuron synthesis. For simplicity here is only displayed a net with N=3.
The number of nodes grows proportional to the number of neurons at maximum topology, but the number of wi or connections grows squared with N'2.
To transform such a neuron as an electronic circuitry the simple differential amp can be used perfectly. It has summable input nodes, its large signal transfer function is almost a tangens hyperbolicus, and it uses only a couple of parts.
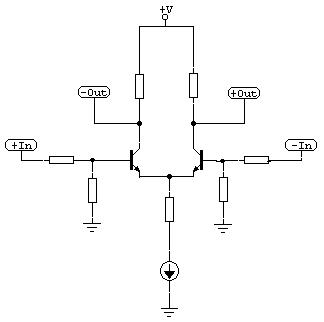
Pic.4
To multiply the pi with the wi we use a potentiometer which wiper position multiplies the input signal with the factor wi. Thus we could form a simple neural net from analog electronic components like in the following pict:
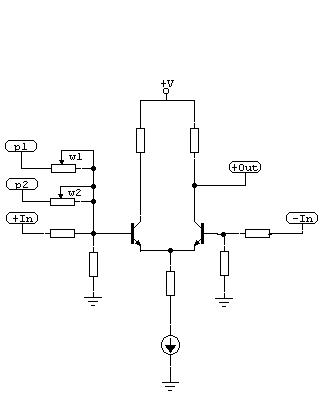
Pic.5
The potentiometer inputs can be extended to any practical number of neuron inputs. Together with R1 they make a voltage divider which upper half is changed in value by the respective potentiometer.
Since they are connected as radial resistors, they sum (or mix) automatically onto R1. Through this an extra resistor per node input can be saved.
However, on the flipside of this arrangement the amount of wi can never be =0 (this refers to Rpot = infinite) or become negative. Furthermore, the mixing potentiometers will not be independent of each other regarding their wiper position. Later more about this topic.
The only question is how to get the "wi" and how they are to be optimized in an actual learning process. The basic intention of a technical neural net in most applications is the recognition of similarities, textures and symmetries with help of "biological intelligence".
But my first goal is not learning by the repetion of something given in the sense of a quality function, but the creativity of the networked itself. For this, it is first necessary to provide the elements and to give the possibility to adjust the parameters without looking for learning processes first. Later on I will give possibilities with the sound code networking to let creative evolutionary processes gain in the resonant net.
Step2. The resonant filter
There has been very much written about filters in electronic sound producers yet. Interesting enough, the steady standing icon of the contemporary synthesizer is the 4 pole filter invented by Robert A. Moog in 1964 and is still the most used and quoted musical filter.
Why is that? Point one, the 4 pole architecture offers enough phase margin to obtain a stable oscillation in the resonant area. Point two, the cutoff slope is made such that it is still musical, because too sharp and cutting filters do not "sound" any more - a filter with a slope of a scy scraper sounds analytic, technical and cold. The resonances that occur in nature are mostly of a 2- to 4- pole kind and they are never too exact, so that our ears are used to that sonic natural environment and feel more comfortable.
The structure of a moog filter is a 4 stage cascade which actually shows up as a differential amp with 4 differential current sources put in series with transversal capacities acting as current controlled RC-stages.
Pic.6
Due to the serial structure of the RC stages the control current fed in by the main current source flows through all of them. So all RC lowpasses have the same corner frequency or cutoff which is controlled by the control current. In the true circuitry, a gain amplifier placed after this stage (not displayed) recovers the gain loss of the filter stages.
The whole circuitry has a further important attribute: The large signal function follows the tangens hyperbolicus (see pic 2). This is often known as "saturation" or distortion and is an important sonic attribute of this filter. Often the typical sound of the moog filter is got by overdriving the filter.
This attribute has a tremendous advantage: in feedback operation the saturation delivers an amplitude regulation which prevents the filter of drifting towards instable states that can easily occur during high resonant leveling.
Step 3. The resonant neuron - Synthesis of step 1 and 2
What appears closer than using this circuitry for a resonant neuron?
Following attributes catalogue just forces one to do it:
- The differential amp is an implicit structure of the filter
- The inputs can sum or mix multiple signal like described above
- It has the tangens hyperbolicus as large signal function. With this, the neuron can also switch and "fire".
- It has enough phase margin to generate clean, by saturation amplitude-regulated sine oscillations and all chaotic transition areas (hint: blowing of a pipe). With this, it is also an oscillator.
- The RC-stages can be seen as information storages to delay the reactions of a neuron for a certain time and providing so time constants for global swing cycles in the net.
- the control parameter cutoff must be seen as an additional branch to make FM modulations possible.
- The filter can gain the net signals, dynamically filter them and act as a source of complex oscillations. With this the terms of threshold switch, amplifier, filter and oscillator melt together to one complex thing, namely the "Resonant Neuron".
We did not yet pay attention for an important further attribute of this filter: The fact that it has an inverting and non-inverting input. In "normal" filter application these inputs are clearly connected. More about this in the next section.
Step 4. Complexity of system dynamics
As is known from the general system dynamics, feedback loops (and the filter itself is such) can have positive and negative kinds of feedback.
The positive ones gain small changes of input signals and bring the system finally to breakdown in a way, that the input value is gained and gained back positively by the feedback and finally leads to an exponential growth at the output. This growth is just limited by the physical rails, in our electronic world by the supply voltage. System dynamics theoreticians would say the positive feedback gains the instabilities of the system and leads to a chaotic non-determinable system reaction. Tiny input changes generate huge output changes.
In contrast to this, the negative feedback stabilises the the system behaviour by subtracting a part of the output signal from the input signal and thus decreases the growth (technically the gain). In regular language usage the word feedback means mostly the negative type which e.g. regulates the non-linearities of complex transfer functions like a transistor amp.
Other examples are the regulation of the sensor-actor system of a robot arm or easier the temperature in a refridgerator. But this is only one side of the coin; in the technical world the most effort is done to limit the instablities = negative feedback.
Related to our filter, it is the negative feedback which brings the filter to resonance. By the phase shift of the RC stages there is one phase that remains because the others are cancelled by phase-inversion - namely the frequency of self-resonance which is the phase where the phase angle is shifted another 180° and which is therefore not dampened but gained. (Because of this the bass drops when the filter is self oscillating in our moog filter. It is a bit compensated by the saturation, but is unavoidable by principle).
But the stabilised system don't represent the whole reality. We did mostly only hear the one side of the sound - the stabilised. A little bit positive feedback in the filter brings totally different sonical attributes than only negative -tiny input signals are drastical highered and gained - totally other sonic results arise from this.
Sound is something that may never be totally reproduceable - then it's dead. Acoustic instruments like a violin have this attribute that the system player/instrument NEVER sounds precisely exactly like the last tone (which makes the listener to beginners mad). The aliveness of true analog sounds is the fact that not everything is able to being calculated or determined to the least detail.
The unbeaten hype for analog synthesizers is an expression for the statement that humans as living beings need also living sounds. Though a lot can be nicely modeled and digitally simulated already, the often spoken word of the digital coldness is just a synonym for the limited number area and therefore resulting problems of modeling chaotic processes in the number domain and the quantised time domain. Not even the simulation of the simple moog filter is possible without major numerical issues because e.g. filter resonance and cutoff are not independent of each other in the number domain - totally different to the analog one.
Life in general is not thinkable without growth (+ feedback) on one hand - exactly like the regulating factors (- feedback) on the other hand which keep it going.
How can an analog circuitry can have the both versions of feedback?
I have implemented a very important circuitry in my opinion - the feedback balance:
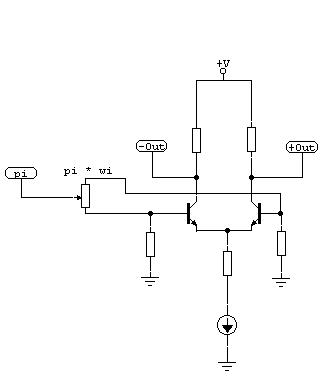
Pic.7
Now you can decide if the net signal pi is positively or negatively coupled to the neuron. If you remember step 1, you will see that now values of 0 or negative ones for the wi are possible. The circuitry is very simple though and lacks additional mixing resistors. It can be cascaded like in pic.5 to the wanted number of summing nodes.
Now you can have e.g. resonances in the network with more neurons than only the own. Also instable toggle swings with several neurons or complex filter sets are possible.
This is the most universal architecture to link the resonant neurons. It is like the integration of a complex formula to a single term.
Normally you would feed an audiosignal in the + input and make the feedback path for resonance into the inverting -input - that is the classical filter architecture. Now it becomes clear why the self-networking related to pic.3 is so important: The regular feedback filter is only a special case of the whole topology.
Namely, if the wi of the own net loop of a neuron becomes negative.
The filter now becomes a system dynamical function block which can do many tasks in the net rather than "only" filter an audio signal. There isn't the expression of adjustable resonance for each filter block any more, but resonance is only achieved if the sum total of feedbacks is more negative than positive - thus multiple filter blocks can co-oscillate in greater net resonance.
Finally the result is always the sum total of the weighting intensitys , if positive or negative. With positive feedback you can achieve toggle swingings like rectangle oscillators or slowly rising LFO-like voltage slopes if the filters break down due to the wanted instabilities and rise again like ramps. All chaotic states between those can swap and change like a caleidoscope. You'll never know where it goes to, but it sounds familiar...
But not enough for this: By the linking of the cutoff signals as a second full network a next net dimension is opened: The frequency modulation.
Step 5. the multiplicative network by FM
Let's summarize: A resonant Neuron sums - like its informational colleague - the input signals together to a threshold function. By the feedback balance the summation can be made positively as negatively - with the corresponding results to the whole system. The RC stages act as information storages like an integrator as well as making the neuron capable of being self resonant (by partly more negative than positive own feedback).
Well, the intensity of integration or better cutoff frequency can be seen as further very important parameter. For this, a further network path as assumed to every neuron which has input from every other neuron - the cutoff or own frequency.
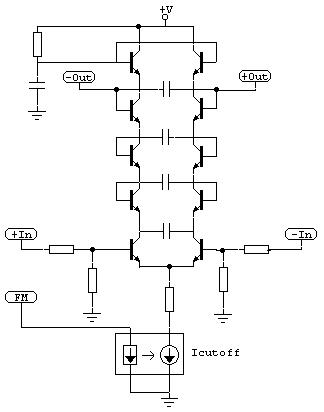
Pic.8
In pict. 8 you can see the additional control input for the control of the superposed cutoff current at the resonant neuron which is named as FM.
The arithmetical command of this combination is quasi the multiplication in the frequency domain or frequency modulation in addition to the additive summation at the differential inputs.
With the resonant neurons, the FM is only one way of each two network branches per neuron. The FM algorithms for the whole network are never given fixed, but are generated by the wwi (I call the multiplicative net intensities "wwi").
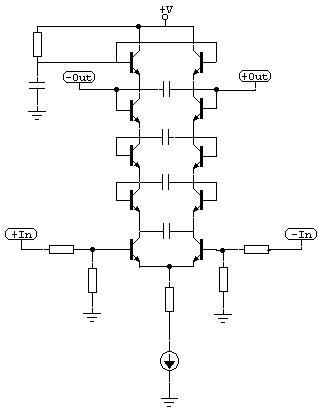
On my first implementation of the resonant Neurons the topology is wholly orthogonal, that means all possible net branches are physically implemented, and the user can decide by giving the intensities which "axons" are used. Therefore, the following picture of the resonant neurons arises:
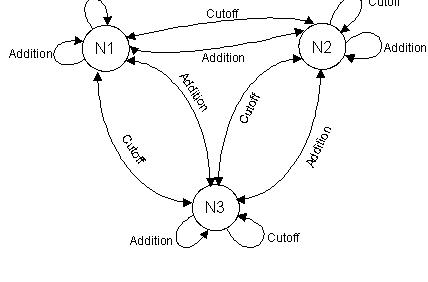
Pic.9
Please note that the connections with double arrows mean that those traces have effect in both directions. That means they are physically double implemented with an wi adjuster per arrow. The self feedback connections (loop arrows) have therefore only one arrow, because each neuron can only once feed back itself.
The outputs of a neuron (which is in real world a sounding signal) can be wether summed on other neurons and be filtered again or resonantly reworked or simply co-oscillate or act as a modulation source for other neurons. The wwi of the cutoff inputs represent in the synthesizer world the amount of a modulation. Corresponding to that, different wwi(amounts) of different neurons (modulation sources) are to be added to the resulting modulation.
The respective addition circuitry for the FM branch of each neuron needs to be implemented. This is a simple Op Amp addition circuitry like in pict. 10.
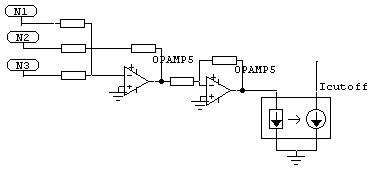
Pic.10
Summary of the analog neuron level
At the RNS, there is no difference between oscillators, filters, modulation sources, LFOs, envelopes and gain amps, but the whole net is generating them in itself automatically by the system dynamics of networked systems.
The whole net makes the sound.
There are no seperate building blocks for separate sections which are linearly connected. Everything influences anything else and is influenced by the others!
FM modulations of single Neurons that are swinging self resonant as co-oscillators in different modes are imagineable like non-linear gain amps that can process an external signal in very complex manner.
The border between sound producer and sound processor fades also. You can also feed external analog signals or control signals into the inputs and process them by the net algorithms in various kinds.
Algorithm means here more an "analog" algorithm which is sourced from the system dynamics of the network and should not be mistaken with a DSP code.
The atual algorithmic part of the resonant neurons is described in the next section.
Step 6. The digital sound code network
How do we get these so far theoretical descriptions together to a working function block?
It seems though as it lacks the "intelligence" to give the function block "resonant neuron" the parameters and let it exchange parameters with the other neurons.
We simply could put the parameter statically on the wi and see, what happens...or we could use an intelligent algorithmic network to let algorithms that itself control the wi let exchange dynamically with other neurons and let them evolve with a certain rate.
Here we arrived at biology, because a genetic code is nothing else but an algorithm. During the biological transscription of a DNA (desoxy ribonuclein acid) section the information is transferred to the RNA (ribo nuclein acid) like a copy and from there synthesized by ribosoms to proteins.
The "characters" ACGT, chained by consecutive base triplets (similar to bytes in computers) are read out like a zipper and re-arranged to a highly complex protein - of course this is a strongly simplified description of the highly complex processes in nature.
But I liked the adaption of this transscription mechanism to the neural sound production. With networked microprocessors you can let similar algorithm patches synthesize to more complex algorithms and let them evolve. One byte carries 256 different informations likewise a base triplet made from 4 characters makes 64 different Informations (but which are not all used).
Those algorithms determine the wi and the wwi of the resonant neurons. But the algorithms can be spontaneously exchanged, mixed up or be replaced among the neurons! They can also mate with other neurons.
In my first physical implementation of the Resonator Neuronium there is a further possibility to feed back the analog world of the neurons to the digital code level by a comparator which is connected to the neuron's output. It switches for inputs smaller than 0 -> 0, greater than 0 -> 1.
With this, the greatest possible flexibility in topology of intermodulative connections of all levels, also the digital domain, can be achieved.
Hereby it is necessary to be able to control the evolutionary rate in a way that leads to optimal results in the wanted synthesis. The analog feedback by the mentioned comparator will do an inportant job to randomize the probabilistic numbers to minimize the effects of numerical randomizing.
Final Summary of Resonant Neuron Synthesis
Now we are complete: A resonant Neuron consists of a 4-pole differential amp filter, which +/- inputs are connected with the other outputs by a feedback balance with the intensity wi.
Furthermore, all ouputs are linked by an addition circuitry with the cutoff frequency inputs of each filter-neuron. Those intensities are the wwi. This is all real analog and is realised with the corresponding transistor circuitries and potentiometers.
The potentiometers are digital controllable to let them be controlled dynamically by an algorithm. This implies the usage of a microprocessor which controls the pots.
I went a step further and gave each neuron its own small microprocessor which is working independently but is connected by serial links with all other neuron processors.
Each neuron processor has the feedback comparator connected to the output of its analog filter neuron so that it gets information about the analog state of the neuron. This will be important regarding to the evolution rate which can be controlled finally analog and thus is not underlying numerical loop effects.
Settings are possible where each zero-crossing of the analog neuron resembles an evolutionary generation. In this moment (quasi a swing- and living cycle) the neuron code is newly recombined with other neurons by mating. So evolving sounds are possible where nobody knows where they will develop to.
One thing is obvious: the adapted life principles will develop them to caleidoscope-like complex "beings" which have to be understood and recognized in a new meaning of art:
Here reigns nature itself with chaos and resonance, oscillation and evolution in an artifical "micro universe" which start- and environmental conditions can be well programmed and stored by the artist.
The algorithms are made such that not only parameter but also full code segments can be exchanged over serial links to make an algorithmic evolution possible or even simply an intelligent interactive processing among the neurons.
Let's let them play together...
Final statement
This all is an extraordinary unusual jump for the average musician.
You can't get back on old experiences, and it is the question anyway if you can produce "usual" tones like with classical polyphonic synthesizers in a normal meaning.
The tension of the Resonant Neuron Synthesis lies in the extreme complexity, the unknownness und the beautiness of the sounds.
Well, just the non-foreseeablility is not wanted by the most musicians who like to have today more then ever a totally controlled and fully determinable studio with total access and total reproduceability.
For those people this kind of sound production is for sure not useful. But I did not design this for them, but instead motivated of my own to let the "classic sound schools" with their total MIDI- and Computer access leave once far behind me.
The sound programming becomes somewhat rather mystical by the net dominance , and you can't rely on linear learnable results like from subtractive synthesizers. Here it is up to experimenting, intuition and patience.
You can say so far: The possibilities and the pure sound substance have something absolutely organic and nature close. They are but unpredictable like the weather which forms entities above us to incredible beautiful new forms and things which are always similar, but never equal. At least, it never becomes boring.
I was first not intersted in a development in commercial dimensions, but in a totally new concept for the production of inspirative sounds and maybe an extension of the contemporay musical art knowing.
It was always annoying to me to walk on beaten tracks, even if this is an important part in live to learn and to know different areas of knowledge.
But one day you have to get up and leave those tracks with the knowing of former experiences to enter new areas in the sense of a co-evolution and combine old components to something new.
By the way, I was inspired to this sound production by the resonance hypothesis of the biologist and nature philosopher Friedrich Cramer.
I wish a lot fun to the interested reader and to possible later users and also fun with the realisation of own ideas and sounds!
© Jürgen Michaelis, August 2000 |